
너비 우선 탐색(BFS)란 무엇인가요?
BFS(Breadth-First Search)는 그래프나 트리 구조를 탐색하는 알고리즘입니다. 이 알고리즘은 시작 노드에서 출발하여 인접한 모든 노드를 먼저 탐색한 후, 다음 레벨의 노드들을 차례로 탐색합니다. BFS는 주로 최단 경로를 찾거나 레벨 순으로 노드를 방문해야 할 때 유용합니다.
BFS의 동작 원리
BFS는 큐(Queue)라는 자료 구조를 사용하여 구현됩니다. 큐는 FIFO(First In, First Out) 방식으로 작동하여 먼저 들어간 것이 먼저 나옵니다. BFS의 기본 동작 과정은 다음과 같습니다.
- 큐 초기화: 시작 노드를 큐에 넣고 방문 표시를 합니다.
- 큐에서 노드 추출: 큐에서 노드를 하나 꺼내어 현재 노드로 설정합니다.
- 인접 노드 확인: 현재 노드와 인접한 모든 노드들을 확인합니다.
- 방문하지 않은 노드 큐에 추가: 인접한 노드 중 방문하지 않은 노드를 모두 큐에 추가하고 방문 표시를 합니다.
- 큐가 빌 때까지 반복: 큐가 빌 때까지 2번부터 4번까지의 과정을 반복합니다.
BFS의 구현 예시
간단한 예제를 통해 BFS의 구현을 살펴보겠습니다. 파이썬 코드로 작성된 BFS 알고리즘은 다음과 같습니다.
import collections
def bfs(graph, start_node):
visited = set() # 방문한 노드를 기록하기 위한 집합
queue = collections.deque([start_node]) # 시작 노드를 큐에 추가
visited.add(start_node) # 시작 노드를 방문 표시
while queue: # 큐가 빌 때까지 반복
node = queue.popleft() # 큐에서 노드를 하나 꺼냄
print(node, end=" ") # 현재 노드를 출력
for neighbour in graph[node]: # 인접한 노드들을 확인
if neighbour not in visited: # 방문하지 않은 노드라면
visited.add(neighbour) # 방문 표시
queue.append(neighbour) # 큐에 추가
# 그래프 예시
graph = {
0: [1, 2],
1: [2],
2: [0, 3],
3: [3]
}
# BFS 탐색 시작
bfs(graph, 0)BFS의 장점
- 최단 경로 찾기: BFS는 무가중치 그래프에서 두 노드 간의 최단 경로를 찾을 수 있습니다.
- 폭넓은 탐색: 모든 레벨의 노드를 차례로 탐색하므로 모든 가능한 경로를 동일하게 고려할 수 있습니다.
- 루프 방지: 이미 방문한 노드를 다시 방문하지 않도록 관리하기 때문에 무한 루프에 빠질 위험이 없습니다.
BFS의 활용 예시
BFS는 여러 실생활 문제에서 활용될 수 있습니다:
- 네트워크 탐색: P2P 네트워크에서 인접 노드를 찾거나, 웹 크롤러가 페이지를 탐색할 때 사용됩니다.
- 경로 탐색: 네비게이션 시스템에서 최단 경로를 찾기 위해 사용됩니다.
- 그래프 분석: 그래프에서 특정 패턴이나 경로를 분석할 때 유용합니다.
- 소셜 네트워크 분석: 소셜 네트워크에서 친구 추천 시스템을 구현할 때 사용됩니다. 예를 들어, 페이스북에서 친구 추천 알고리즘에 BFS가 사용될 수 있습니다.
- 인공지능: 게임 AI에서 경로 찾기 알고리즘으로 사용됩니다. 예를 들어, 체스 게임에서 말의 이동 경로를 계산할 때 BFS가 사용될 수 있습니다.
BFS 알고리즘 동작 예시
다음 이미지는 BFS 알고리즘이 그래프에서 어떻게 동작하는지를 단계별로 시각적으로 보여줍니다. 이 예시는 BFS가 노드 0에서 시작하여 그래프의 모든 노드를 탐색하는 과정을 나타냅니다. 각 단계에서 큐(Queue)의 상태와 탐색 중인 노드들을 볼 수 있습니다.
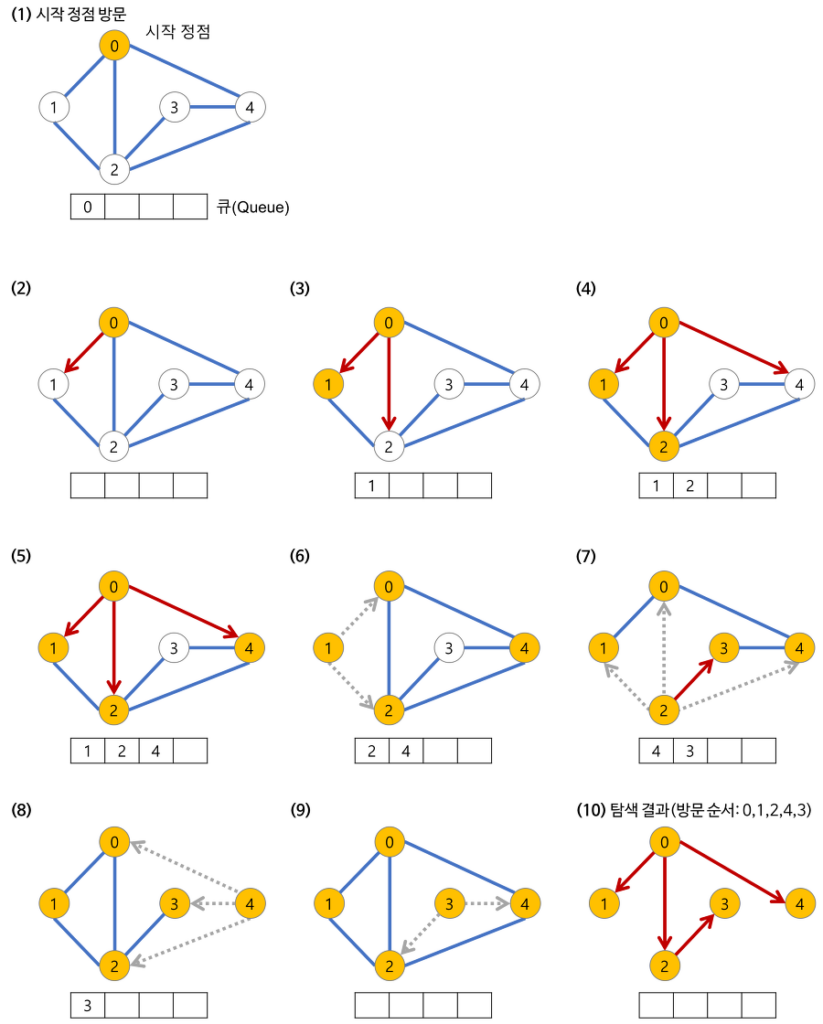
단계별 설명:
- 초기 상태:
- 노드 0이 시작점입니다.
- 큐에는 시작 노드인 0만 들어 있습니다.
- 큐: [0]
- 1단계:
- 노드 0을 방문하고 큐에서 제거합니다.
- 노드 0의 인접 노드들(1, 2, 4)을 큐에 추가합니다.
- 방문 순서: 0
- 큐: [1, 2, 4]
- 2단계:
- 노드 1을 방문하고 큐에서 제거합니다.
- 노드 1의 인접 노드(0)는 이미 방문했으므로 추가하지 않습니다.
- 방문 순서: 0, 1
- 큐: [2, 4]
- 3단계:
- 노드 2를 방문하고 큐에서 제거합니다.
- 노드 2의 인접 노드(0, 3, 4) 중 방문하지 않은 노드 3을 큐에 추가합니다.
- 방문 순서: 0, 1, 2
- 큐: [4, 3]
- 4단계:
- 노드 4를 방문하고 큐에서 제거합니다.
- 노드 4의 인접 노드(0, 2)는 이미 방문했으므로 추가하지 않습니다.
- 방문 순서: 0, 1, 2, 4
- 큐: [3]
- 5단계:
- 노드 3을 방문하고 큐에서 제거합니다.
- 노드 3의 인접 노드(2)는 이미 방문했으므로 추가하지 않습니다.
- 방문 순서: 0, 1, 2, 4, 3
- 큐: [] (빈 큐)
이 과정을 통해 BFS 알고리즘은 그래프의 모든 노드를 레벨 순으로 방문하게 됩니다.
BFS 알고리즘의 핵심 포인트
- 큐 사용: BFS는 큐를 사용하여 노드를 순차적으로 탐색합니다.
- 방문 관리: 이미 방문한 노드를 다시 탐색하지 않도록 관리합니다.
- 레벨 순 탐색: 한 레벨의 모든 노드를 탐색한 후, 다음 레벨로 넘어갑니다.
결론
BFS 알고리즘은 그래프나 트리 구조를 탐색하는 데 있어 매우 유용한 도구입니다. 큐를 사용하여 레벨 순으로 노드를 방문함으로써 효율적이고 체계적으로 탐색을 수행할 수 있습니다. BFS는 네트워크 탐색, 경로 찾기, 그래프 분석 등 다양한 분야에서 활용될 수 있으며, 알고리즘의 원리를 이해하고 이를 적절히 응용하는 것이 중요합니다. BFS를 통해 복잡한 문제를 효과적으로 해결할 수 있으며, 다양한 실생활 응용 사례를 통해 그 유용성을 확인할 수 있습니다.
'CS > 알고리즘' 카테고리의 다른 글
| [Algorithm/알고리즘] Greedy - 그리디 알고리즘(탐욕법) 이해하기 (0) | 2025.05.21 |
|---|---|
| [Algorithm/알고리즘] Trie - 트라이 자료구조 이해하기 (1) | 2025.05.21 |
| [Algorithm/알고리즘] LCA - 최소 공통 조상 알고리즘 이해하기 (1) | 2025.05.21 |
| [Algorithm/알고리즘] DFS - 깊이 우선 탐색 알고리즘 이해하기 (0) | 2025.05.21 |
| [Algorithm/알고리즘] Backtracking - 백트래킹 알고리즘 이해하기 (0) | 2025.05.21 |



